Subproject 6: Constraining the interiors of exoplanets by measuring the Love number k2
PIs: H. Rauer and S. Csizmadia, PhD: H. Hellard
Summary
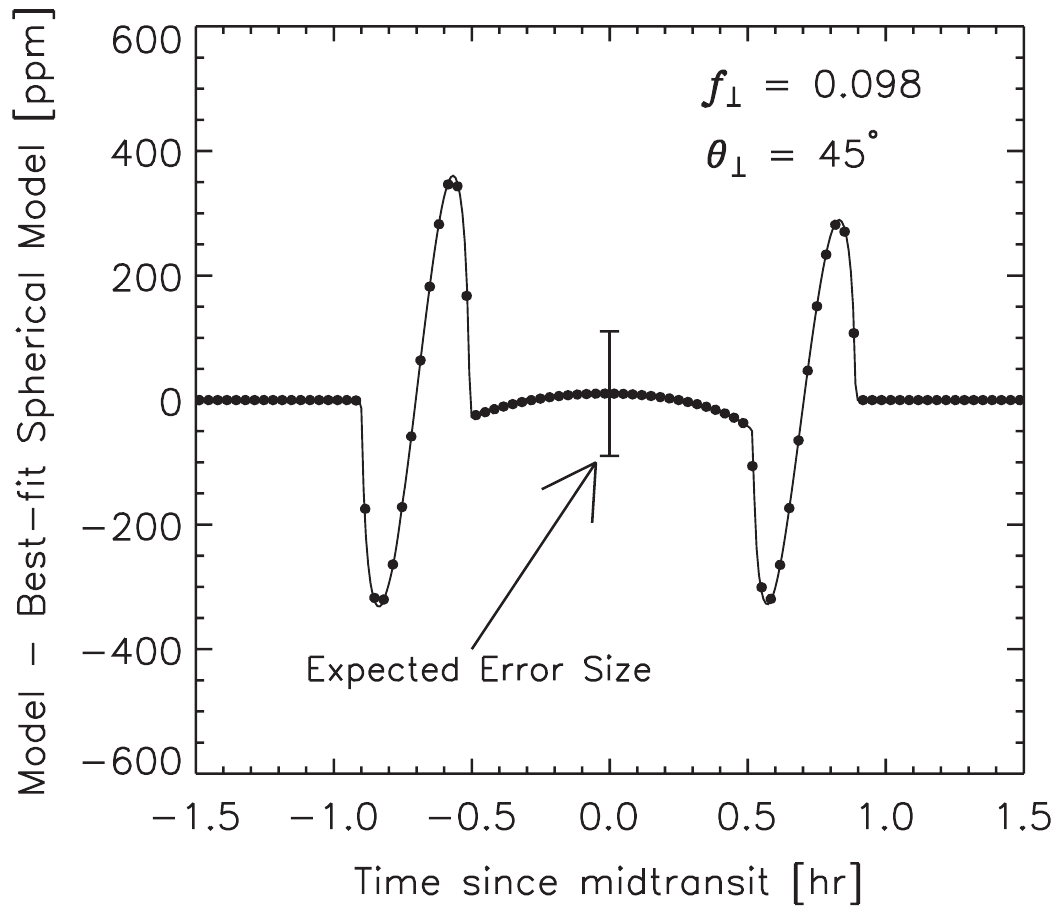
Exoplanets are one of the most exciting kind of celestial objects and they are in the forefront of public interest. Direct measurements of polar flattening of exoplanets taking into account quite a number of additional effects (limb darkening, realistic density distributions beyond mass-point approximations, radiation pressure etc.) has never been attempted before. Such software tools and results will help to advance our knowledge about the interiors and compositions of exoplanets.
We will develop a new software package to model transit light curves of exoplanets with tidally and rotationally distorted components. This work is starting from an already existing code based on the Roche-model (which consists of a massless, but emitting and/or reflecting, tidally and rotationally distorted envelope, and a core in the center of the celestial object that contains the entire mass of the object). Such a model was found to be appropriate for main sequence stars. The code will be modified to make it appropriate for exoplanets. Therefore, it will be extended by non-homogeneous internalmass distribution components and it will take into account the radiation pressure caused by the host star because this is important for close-in exoplanets with extended, dense atmospheres. Since gravitational microlensing in the binary system of the planet (lense) and star (source) is thought to contribute to the observed light curve distortions, we plan to add this effect into the code. Limb darkening will be an adjustable parameter independent of existing stellar atmosphere models, but we plan to allow the user the possibility to modify this for a given stellar atmosphere model. We will improve our existing code to include stellar variability phenomena by developing and adding a red-noise (autoregressive and/or Gaussian Process) model. Then the code will be able to determine the ratio of the polar and the equatorial radii of the transiting exoplanet from a measured transit light curve.
In addition, we will perform studies on applicability of multicolour photometry. Observations obtained at different wavelengths may help to resolve the degeneracy between different parameters.
Finally, the measured polar flattening values will be linked to the internal structure of the exoplanet. This requires knowledge of the rotational period of the exoplanet. To first approximation, we assume that the closest exoplanets are tidally locked. A more sophisticated estimate can be based on the shape-distortion, because the centrifugal force is axially symmetric while tidal forces have a characteristic orientation. The code will be able to separate these effects.
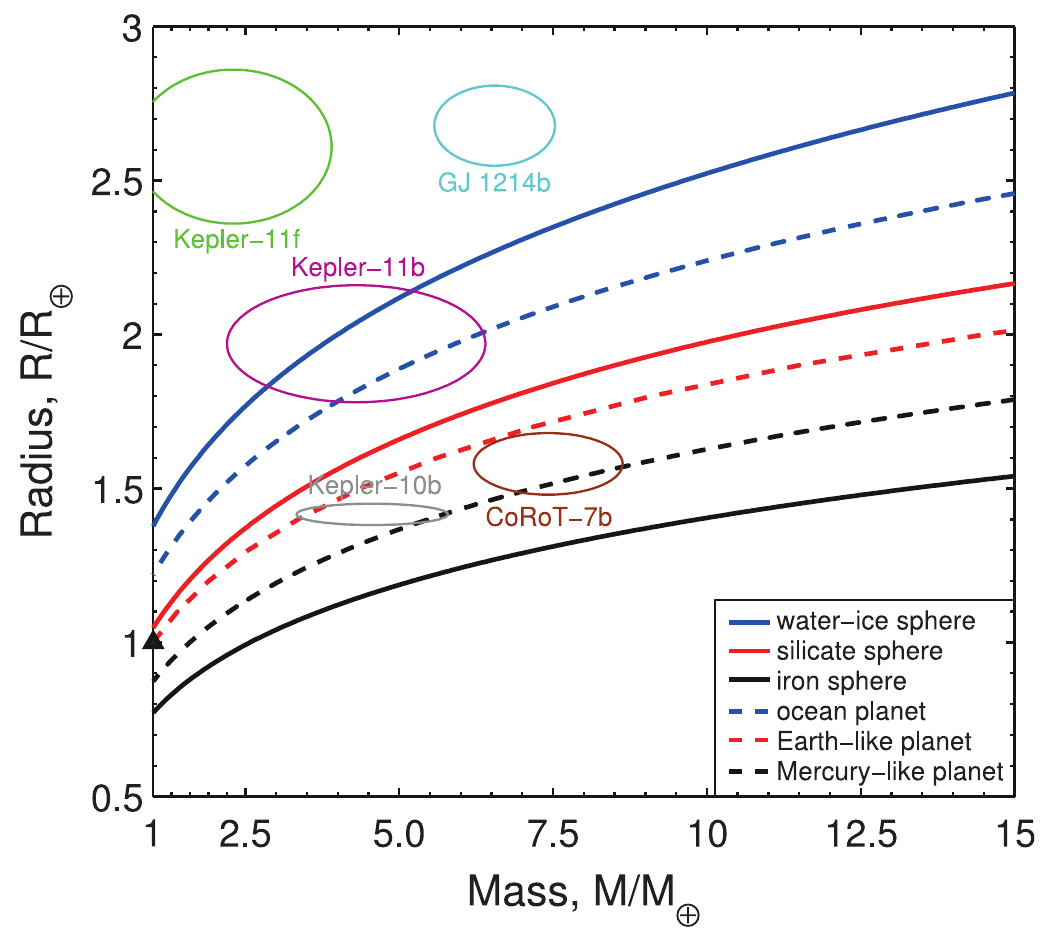
The expected result of SP6 is an estimate of the polar flattening of several exoplanets and constraints for the rotational period, gravitational quadrupole moment J2 and Love number k2,f. These numbers can be compared to theoretical expectations and thus can be used for further refinement of our knowledge on exoplanets’ interiors.
The interior models of SP4 and SP5 based on EoS data obtained by SP1-3 and SP7-9 can be used as initial estimates in our work. Then we can make predictions concerning which kind of light curve distortions can be observed. A comparison of the observed data and our model calculations may allow us to refine the k2,f Love number values and giving a feedback about the observability of polar flattening as well as the code will be able to constrain this interior structure parameter.